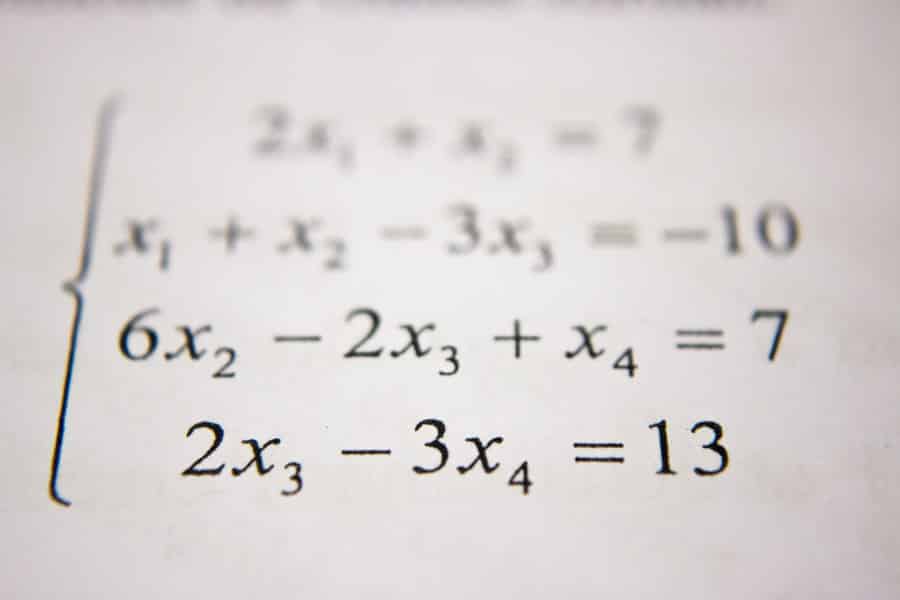50 IB Maths IA Topic Ideas

IB Maths is a struggle for most people going through their diploma. To make matters worse, on top of just doing the dreaded maths exam, we’re also expected to write a Maths IA exploration into a topic of our choice! Where do you even begin such a task? How do you even choose a topic? To make things easier, we have plenty of free Maths resources! Firstly though, we’ve compiled 50 common Maths IA topics that may spark some creative juices and set you on your way to conquering one of the hardest assignments of the diploma!

Once you have chosen your topic, you may want to check out our other posts on how to structure and format your Maths IA or how to write your IA.

NOTE: These topics are purely meant as inspiration and are not to be chosen blindly. Even though many of these topics led to high scores for some of our graduates in the past, it is important that you listen to the advice of your subject teacher before choosing any topic!

1-10

• Pascal’s triangle: Discovering patterns within this famous array of numbers
• Pythagorean triples: Can you find patterns in what numbers form a pythagorean triple?
• Monty Hall problem: How does Bayesian probability work in this real-life example, and can you add a layer of complexity to it?
• The Chinese Remainder Theorem: An insight into the mathematics of number theory
• Sum of all positive integers is -1/12? Explore this fascinating physics phenomenon through the world of sequences and series
• Birthday paradox: Why is it that in a room of people probability dictates that people are very likely to share a birthday? 
• Harmonic series: Explore why certain notes/chords in music sound dissonant, and others consonant, by looking at the ratios of frequencies between the notes.
• Optimizing areas: Optimizing the area of a rectangle is easy, but can you find a way to do it for any polygon?
• Optimizing volumes: Explore the mathematics of finding a maximum volume of a cuboid subject to some constraint
• Flow of traffic: How does mathematics feed into our traffic jams that we endure every morning?

11-20

• Football statistics: Does spending a lot of cash during the transfer window translate to more points the following year? Or is there a better predictor of a team’s success like wages, historic performance, or player valuation?
• Football statistics #2: How does a manager sacking affect results? 
• Gini coefficient: Can you use integration to derive the gini coefficient for a few countries, allowing you to accurately compare their levels of economic inequality?
• Linear regressions: Run linear regressions using OLS to predict and estimate the effect of one variable on another.
• The Prisoner’s Dilemma: Use game theory in order to deduce the optimal strategy in this famous situation
• Tic Tac Toe: What is the optimal strategy in this legendary game? Will my probability of winning drastically increase by some move that I can make?
• Monopoly: Is there a strategy that dominates all others? Which properties should I be most excited to land on?
• Rock Paper Scissors: If I played and won with rock already, should I make sure to change what I play this time? Or is it better to switch? 
• The Toast problem: If there is a room of some number of people, how many toasts are necessary for everyone to have toasted with everyone?
• Cracking a Password: How long would it take to be able to correctly guess a password? How much safer does a password get by adding symbols or numbers?

21-30

• Stacking Balls: Suppose you want to place balls in a cardboard box, what is the optimal way to do this to use your space most effectively?
• The Wobbly Table: Many tables are wobbly because of uneven ground, but is there a way to orient the tables to make sure they are always stable?
• The Stable Marriage Problem: Is there a matching algorithm that ensures each person in society ends up with their one true love? What is the next best alternative if this is not viable?
• Mathematical Card Tricks: Look at the probabilities at play in the famous 3 card monte scam. 
• Modelling the Spread of a Virus: How long would it take for us all to be wiped out if a deadly influenza spreads throughout the population?
• The Tragedy of the Commons: Our population of fish is dwindling, but how much do we need to reduce our production by in order to ensure the fish can replenish faster than we kill?
• The Risk of Insurance: An investigation into asymmetric information and how being unsure about the future state of the world may lead us to be risk-averse
• Gabriel’s Horn: This figure has an infinite surface area but a finite volume, can you p
  rove this?
• Modelling the Shape of an Egg: Although it may sound easy, finding the surface area
  or volume of this common shape requires some in-depth mathematical investigation
• Voting Systems: What voting system ensures that the largest amount of people get the official that they would prefer? With 2 candidates this is logical, but what if they have more than 2?

31-40

• Probability: Are Oxford and Cambridge biased against state-school applicants?
• Statistics: With Tokyo 2020 around the corner, how aboutmodelling change in record performances for a particular discipline?
• Analysing Data: In the 200 meter dash, is there an advantage to a particular lane in track? 
• Coverage: Calculation of rate of deforestation, and afforestation. How long will our forests last?
• Friendly numbers, Solitary numbers, perfect numbers: Investigate what changes the condition of numbers
• Force: Calculating the intensity of a climber’s fall based upon their distance above where they last clamped in
• Königsberg bridge problem: Using networks to solve problems. 
• Handshake problem: How many handshakes are required so that everyone shakes hands with all the other people in the room? 
• The mathematics of deceit: How con artists use pyramid schemes to get rich quick!
• Modelling radioactive decay: The maths of Chernobyl – when will it be safe to live there?

41-50

• Mathematics and photography: Exploring the relationship between the aperture of a camera and a geometric sequence
• Normal Distribution: Using distributions to examine the 2008 financial crisis
• Mechanics: Body Proportions for Track and Field events
• Modelling: How does a cup of Tea cool?
• Relationships: Do BMI ratings and country wealth share a significant relationship?
• Modelling: Can we mathematically model musical chords and concepts like dissonance?
• Evaluating limits: Exploring L’Hôpital’s rule
• Chinese postman problem: How do we calculate shortest possible routes?
• Maths and Time: Exploring ideas regarding time dilation
• Plotting Planets: Using log functions to track planets!

So there we have it: 50 IB Maths IA topic ideas to give you a head-start for attacking this piece of IB coursework! We also have similar ideas for Biology, Chemistry, Economics, History, Physics, TOK… and many many more tips and tricks on securing those top marks on our free resources page – just click the ‘Maths resources’ button!

Still feeling confused, or want some personalised help? We offer online private tuition from experienced IB graduates who got top marks in their Maths IA.